系统,控制与应用数学
Laplace 变换
控制系统(现代部分)
控制系统的基本单元
比例环节 \[G(s) = k_p\]
惯性环节 \[G(s) = \frac{1}{Ts+1}\] \(h(t) = 1-e^{-\frac{t}{T}}\) 单位阶跃响应为指数曲线
二阶震荡环节 \[G(s) = \frac{1}{T^2s^2+2\xi Ts+1}\] \(T\) 为时间常数,\(\xi\) 为阻尼系数
\(s_1,2 = -\frac{\xi}{T} \pm \frac{\sqrt{\xi^2-1}}{T}\)
- \(\xi = 0\) 无阻尼,无衰减振荡,一对纯虚根
- \(0<\xi<1\) 欠阻尼,衰减振荡,一对共轭复根
- \(\xi = 1\) 临界阻尼,单调衰减,相等负实根
- \(\xi > 1\) 过阻尼,无振荡,两个不相等的实根
积分环节 \[G(s) = \frac{k_i}{s}\]
延迟环节 \[G(s) = e^{-\tau s}\]
微分环节 \[G(s) = k_d s\] \[G(s) = Ts+1\] \[G(s) = T^2s^2+2\xi Ts+1\]
状态空间
\[\begin{cases} \dot{x} = Ax+Bu \\ y = Cx(+Du) \end{cases}\]
- \(x(t)\) 为状态向量,\(u(t)\) 为输入向量,\(y(t)\) 为输出向量
- 状态变量个数等于系统独立储能元件个数,即系统阶数
- 状态方程\(\dot{x} = Ax+Bu\) 描述系统状态变量的变化,输出方程\(y = Cx+Du\) 描述系统输出与状态变量的关系
传递函数阵
对状态方程和输出方程进行拉普拉斯变换
\[\begin{cases} X(s) = (sI-A)^{-1}BU(s) \\ Y(s) = C(sI-A)^{-1}BU(s)+DU(s) \end{cases}\]
得到传递函数阵
\[G(s) = C(sI-A)^{-1}B+D\]
组合系统传递函数阵
- 并联:\(G(s) = G_1(s)+G_2(s)\)
- 串联:\(G(s) = G_2(s)G_1(s)\)(注意顺序)
- 反馈:\(G(s) = G_1(s)\cdot[I+G_2(s)G_1(s)]^{-1}\)
状态空间的实现
本质是找状态变量
- 串并联分解至最小单元(积分单元),系统框图-->状态方程
- 部分分式分解(留数分解),得Jordan标准型
- 基于积分器串联+常值反馈,得到能控、能观标准型,二者互为对偶
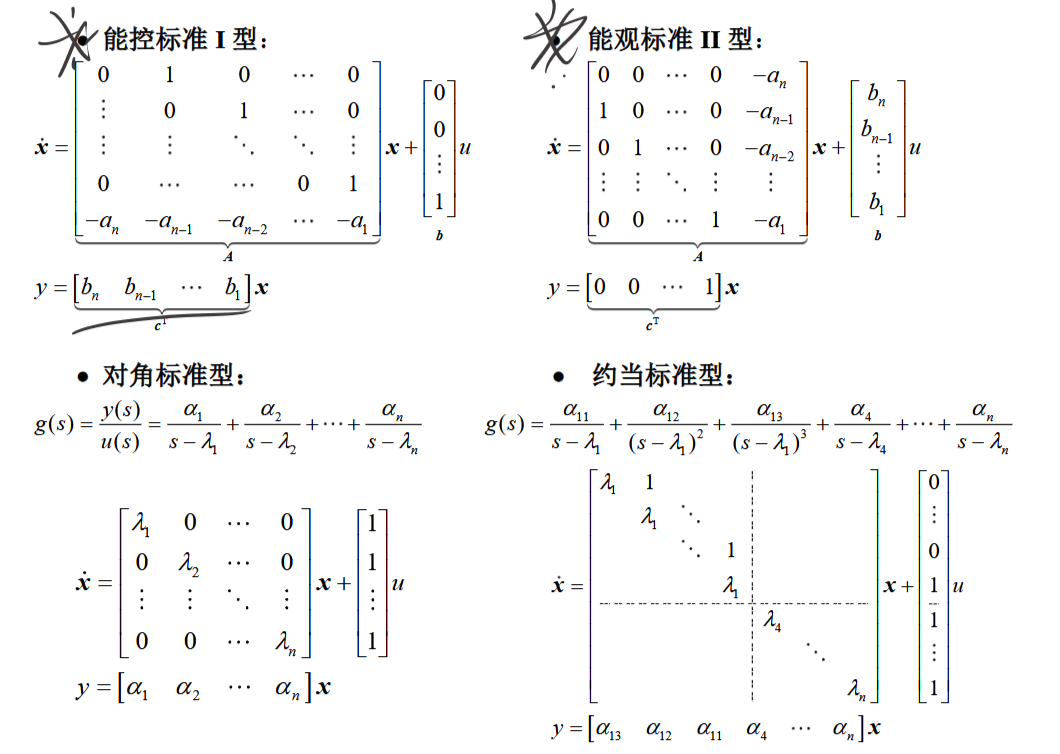
标准型
能控标准型,能观标准型
对角标准型,Jordan标准型
系统的等价变换
对于系统[1]
\[\begin{cases} \dot{x} = Ax+Bu \\ y = Cx+Du \end{cases}\]
进行坐标线性变换\(x = Tz\)或\(z = T^{-1}x\),得到新的状态方程
\[\begin{cases} \dot{z} = T^{-1}ATz+T^{-1}Bu \\ y = CTz+Du \end{cases}\]
令
\[\begin{cases} A' = T^{-1}AT ,\ B' = T^{-1}B \\ C' = CT ,\ D' = D\\ \end{cases}\]
则新的状态方程[2]为
\[\begin{cases} \dot{z} = A'z+B'u \\ y = C'z+D'u \end{cases}\]
[1]和[2]在代数上等价
系统特征值(状态矩阵\(A\)的特征值\(\lambda\), \(|\lambda I-A| = 0\))、特征多项式、传递函数阵在等价系统中具有相同形式
特征向量:\(AP_i = \lambda_iP_i\),\(P_i\)为矩阵\(A\)的对应于特征值\(\lambda_i\)的特征向量
状态空间表达式变换为标准型
- 矩阵有两两相异特征值,可通过\(z = T^{-1}x\)变换为对角型,\(T = [P_1,P_2,\cdots,P_n]\)特征向量矩阵
- 矩阵有重特征值,仍可迭代计算求出能变换为Jordan标准型的特征向量矩阵\(T\),从而变换为Jordan标准型
线性系统状态方程的解(时域分析)
矩阵指数:\(\phi(t) = e^{At}\)
- 定义式:\(e^{At} = I + At + \frac{A^2t^2}{2!} + \cdots\) = _{k=0}^{} $
- 反Laplace变换:\(e^{At} = \mathcal{L}^{-1}\{[sI-A]^{-1}\}\)
线性连续定常系统状态方程\(\dot{x} = Ax+Bu\)的解:
\(x(t) = e^{At}x(0)+\int_0^t e^{A(t-\tau)}Bu(\tau)d\tau\),
- 自由解\(x_f(t) = e^{At}x(0)\),为初始时刻状态向量到\(t\)时刻的状态向量的变换,矩阵指数\(e^{At}\)为状态转移矩阵
- 强迫解\(x_p(t) = \int_0^t e^{A(t-\tau)}Bu(\tau)d\tau\),从时域上看为状态转移矩阵\(e^{At}\)与输入信号\(Bu(t)\)的卷积
- 可通过Laplace变换,两边从变换域解方程:\(x(s) = [sI-A]^{-1}x(0)+[sI-A]^{-1}Bu(s)\)
状态转移矩阵的性质
- 大多数直接用级数展开定义式推导即可,很符合直觉
- 对角标准型、Jordan型可变换